on
Performance Puzzler: The Slow Server
In the spirit of the TCP Puzzlers, I want to present a small distributed systems performance puzzler: In a distributed system with a fixed-number of servers and a fixed concurrency, what happens when one of the backend servers gets slow? First, let’s pick apart what this means.
Suppose you have:
- a service with a fixed number of backend servers – say, 100 servers – each exactly equivalent. You could imagine this as a load balancing service having 100 backends or a key-value store having 100 well-distributed shards.
- a fixed number of clients – say, 10,000. Each client makes one request to the system at a time. When each request completes, the client makes another one. The 10,000 clients could be 1,000 clients each having a 10-way thread pool or 10 event-oriented clients each capable of 1,000 concurrent requests – either way, the total concurrency is 10,000. It doesn’t matter of the clients and server communicate via RPC, HTTP, or something else.
with the following assumptions (which we’ll revisit later):
- All requests take about the same amount of work to process, both on the client-side and server-side.
- The per-request cost outside the server is negligible. (We’re going to ignore client-to-server transit time as well as client processing time.)
- The backend servers are infinitely scalable. That is, we’ll assume that if they take 1ms to process 1 request, they’ll also take 1ms to process 10 requests issued at the same time.
- Each request is dispatched to one of the servers uniformly at random.
To start with, suppose each server takes 1ms to complete each request. What’s the throughput of the entire system? What will be the per-server throughput?
There are a few ways to analyze this:
- From the client perspective, we know there will be 10,000 requests outstanding to the system at any given instant. (Remember, there are 10,000 clients, each making a single request at a time, and we’re assuming zero per-request costs on the client side and in transit.) After 1ms, those requests have all completed and another 10,000 requests are running. At this rate, the system will complete (10,000 requests per millisecond) times (1,000 milliseconds per second) = 10 million requests per second. Intuitively, with all servers equal, we’d expect each server to be handling 1% of these, or 100,000 requests per second.
- From the server perspective: with 10,000 outstanding requests at all times and 100 servers, we’d expect about 100 requests outstanding per server at all times. Each takes 1ms, so there would be 100,000 completed per server per second (which matches what we said above).
Now, what happens when one of the servers becomes slow? Specifically, suppose all of a sudden one of the servers starts taking 1s to process every request. What happens to overall throughput? What about per-server throughput? (Make a guess before reading on!)
The analysis is a bit more complex than before. From the client perspective, there will still always be 10,000 requests outstanding. 99% of requests will land on a fast server and take 1ms, while the remaining 1% will land on the slow server and take 1s. The expected latency for any request is thus 0.99 * 1ms + 0.01 * 1000ms = 10.99ms. If each of the 10,000 clients completes (1 request / 10.99ms) times (1,000 milliseconds per second), we get an expected throughput of about 91 requests per client, or 909,918 requests per second. (That’s a degradation of 91% from the original 10 million requests per second!)
Above, we assumed that each server had the same throughput, but that’s not so obvious now that one of them is so slow. Let’s think about this another way on the client side: what’s the probability at any given time that a client has a request outstanding to the slow server? I find it easiest to imagine the assignment being round-robin instead of random. Suppose clients issued requests to each of the 99 fast servers, then the slow server, and then started again with the first fast server. In that case, the first 99 requests would take 99ms, and the last request would take 1s. The client would have a request outstanding to the slow server for 1,000 ms / 1,099 ms or about 91% of the time. There’s a more rigorous explanation below, but I think it’s intuitive that the random distribution of work would behave the same way on average.
In that case, we could also expect that 91% of clients (or 9100 clients) have a request outstanding to the slow server at any given time. Each of these takes 1 second. The result is a throughput of 9,100 requests per second on the slow server.
What about the fast server? We’d expect that each fast server has 1/99 of the remaining requests (9% of requests) at any given time, which works out to 9.1 requests per server. At 1ms per request, these servers are doing (drum roll) 9,100 requests per second. The same as the slow server! Is that what you guessed? I didn’t.
This isn’t an accident of the specific numbers I picked. If you run the same analysis algebraically instead of with concrete numbers, you’ll find that the general result holds: in this system, when one server becomes slow, the throughput of every server remains the same.
A (more) formal proof
Let’s define some notation:
- C: the total client concurrency (10,000 in our example)
- N: the number of servers (100 in our example)
- Si: server
i(whereiranges from 1 to N) - Li: the latency (in seconds) of requests to server Si. In our example, L1 would be 1 second, while Lj = 0.001 for j > 1.
- Ci: the number of requests outstanding on server Si at any given time.
- Ti: the throughput of server Si (in requests per second).
- Pr(ci): the probability that a particular client has a request outstanding to server Si at any given time.
- Pr(Ri): the probability that a newly-issued request will be issued to server Si.
We’re looking for a formula for Ti. For a server that can handle one request a time, the throughput is simply the inverse of the latency (1/Li). We said that our server was infinitely scalable, which means it can execute an arbitrary number of requests in parallel. Specifically, it would be executing Ci requests in parallel, so the throughput Ti is:

Now, how do we calculate Ci, the concurrency of requests at each server? Well, since each client has exactly one request outstanding at a time, Ci is exactly the number of clients that have a request outstanding to server Si. Since the clients operate independently, that’s just:

To calculate ci, we need the percentage of time that each client has a request outstanding to Si. We define a probability space of events (t, i) indicating that at millisecond timestamp t, the client has a request outstanding to server Si. By simply counting the events, we can say that the probability that a client has a request outstanding to server Si is:
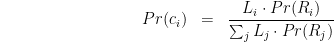
Now, since it’s equally likely that we’ll assign any given request to any server:

that means:
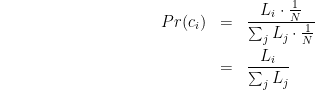
All we’re saying here is that the fraction of time each client spends with a request outstanding to a particular server is exactly that server’s latency divided by the latency of all servers put together. This makes intuitive sense: if you have 20 servers that all take the same amount of time, each client would spend 5% (1/20) of its time on each server. If one of those servers takes twice as long as the others, it will spend 9.5% (2/21) of its time on that one (almost twice as much as before) and 4.8% (1/21) on the others.
With this, we can go back to Ci:


and finally back to Ti:
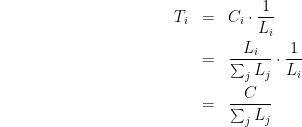
and we have our result: the throughput at each server does not depend at all on the latency of that server (or any other server, for that matter)!
We can plug in some numbers to sanity check. In our example, we started with:
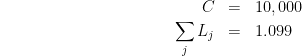
and we get the results:
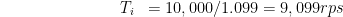
which matches what we said above.
Simulating the behavior
One might find this result hard to believe. I wrote a simple simulator to demonstrate it. The simulator maintains a virtual clock with a 1ms resolution. To start with, each client issues a request to a random server. Each virtual millisecond, the simulator determines which requests have completed and has the corresponding clients make another request. This runs for a fixed virtual time, after which we determine the total throughput and the per-server throughput.
The simulator as-is hardcodes the the scenario that I described above (1 server with 1s per request, 99 servers with 1ms per request) and a 10-minute simulation. For the specific numbers I gave earlier, the results are:
$ node sim.js
simulated time: 600000 ms
total client concurrency: 10000
servers:
1 server that completes requests with latency 1000 ms (starting with "server_0")
99 servers that complete requests with latency 1 ms (starting with "server_1")
server_0 5455039 requests ( 9092 rps)
server_1 5462256 requests ( 9104 rps)
server_2 5459316 requests ( 9099 rps)
server_3 5463211 requests ( 9105 rps)
server_4 5463885 requests ( 9106 rps)
server_5 5456999 requests ( 9095 rps)
...
server_95 5457743 requests ( 9096 rps)
server_96 5459207 requests ( 9099 rps)
server_97 5458421 requests ( 9097 rps)
server_98 5458234 requests ( 9097 rps)
server_99 5456471 requests ( 9094 rps)
overall: 545829375 requests (909715 rps, expect 9097 rps per server)
In my simulations, server_0 is generally a bit slower than the others, but within 0.2% of the overall overage. The longer I run the simulation, the closer it gets to the mean. Given that the slow server is three orders of magnitude slower per request (1s vs. 1ms), I’d say it’s fair to conclude that the per-server throughput does not vary among servers when one server is slow.
Conclusions
The main result here is that in this system, the per-server throughput is the same for all servers, even when servers vary significantly in how fast they process requests. While the implementations of servers may be independent (i.e., they share no common hardware or software components), their behavior is not independent: the performance of one server depends on that of other servers! The servers have essentially been coupled to each other via the clients.
This result implies another useful one: in a system like this one, when overall throughput is degraded due to one or more poorly-performing servers, you cannot tell from throughput alone which server is slow – or even how many slow servers there are! You could determine which server was slow by looking at per-server latency.
Note too that even when this system is degraded by the slow server, the vast majority of requests complete very quickly. At the same time, clients spend the vast majority of their time waiting for the slow server. (We’ve come to refer to this at Joyent as “getting Amdahl’d”, after Amdahl’s Law.)
If you found this result surprising (as I did), then another takeaway is that the emergent behavior of even fairly simple systems can be surprising. This is important to keep in mind when making changes to the system (either as part of development or in production, as during incident response). Our intuition often leads us astray, and there’s no substitute for analysis.
What about those assumptions?
The assumptions we made earlier are critical to our result. Let’s take a closer look.
- “There are a fixed number of clients.” This is true of some systems, but certainly not all of them. I expect the essential result holds as long as client count is not a function of server performance, which probably is true for many systems. However, if client software responds to poor performance by either reducing concurrency (figuring they might be overloading the server) or increasing it (to try to maintain a given throughput level), the behavior may well be different.
- “All requests take about the same amount of work to process, both on the client-side and server-side.” This is true of some systems, but not others. When the costs differ between requests, I’d expect the actual per-client and per-request throughput to vary and make the result shown here harder to see, but it doesn’t change the underlying result.
- “The per-request cost outside the server is negligible.” This isn’t true of real systems, but makes the math and simulation much simpler. I expect the results would hold as long as the per-request client and transit costs were fixed and small relative to the server cost (which is quite often true).
- “The backend servers are infinitely scalable. That is, we’ll assume that if they take 1ms to process 1 request, they’ll take 1ms to process 10 requests issued at the same time.”. This is the most dubious of the assumptions, and it’s obviously not true in the limit. However, for compute-bound services, this is not an unreasonable approximation up to the concurrency limit of the service (e.g., the number of available threads or cores). For I/O bound services, this is also a reasonable approximation up to a certain point, since disks often work this way. (For disks, it may not take much longer to do several read or write I/Os – even to spinning disks – than to do one such I/O. The OS can issue them all to the disk, and the disk can schedule them so they happen in one rotation of the platter. It’s not always so perfect as that, but it remains true that you can increase the concurrent I/O for disks up to a point without significantly increasing latency.)
- “Each request is dispatched to one of the servers uniformly at random.” Many client libraries (e.g., for RPC) use either a random-assignment policy like this one or a round-robin policy, which would have a similar result. For systems that don’t, this result likely won’t hold. In particular, a more sophisticated policy that keeps track of per-server latency might prefer the faster servers. That would send less work to the slower server, resulting in better overall throughput and an imbalance of work across servers.
As you can see, the assumptions we made were intended to highlight this particular effect – namely, the way a single slow server becomes a bottleneck in clients that affects throughput on other servers. If you have a real-world system that looks at all similar to this one and doesn’t have a more sophisticated request assignment policy, then most likely this effect is present to some degree but it maybe harder to isolate relative to other factors.